Think for a moment about your chest of tools as an architect, engineer, or designer. You have a variety of software systems, years of experience, and training. Experience tells you when things won’t work well, like that element can’t go there, it will cause a clash. If you are new to BIM, drafting in 3D, or using Dynamo, this probably sounds like a bright future, but how do you get to that level?
Logic, your intangible building block
Just like speaking a language, knowing what a statement or operator does before you use it is half the battle. You may know all the Spanish words in the world, but you need to know the right time to use them, what order they go in, and what responses to give when you are ordering dinner. Knowing your doctors office vocabulary doesn’t go very far if you just want a glass of wine and some tapas.
Writing software is no different, so first, let’s start with a little bit of metaphysics. What is this “Experience” I mentioned in the first paragraph and how do you get there as quickly as possible if you are just getting started?
Symbolizing your thoughts
| Think for a minute if I told you my shirt is “Not Red.”
What color is it? What is “Not Red.” Ok, so you understand. Maybe. You do not yet know the truthful statement that my shirt is grey. But, you also know that my shirt might be grey.
What if I said my shirt is “grey or blue”? Now you know it certainly isn’t red, yellow, teal, or tan. We could use similar logic orally to give truthful statements by combining what we already know. My shirt is either grey or not red. My shirt is not yellow. My shirt is not green or yellow. If my shirt is grey, then it’s not teal.
If this is confusing, or you are wondering what shirts have to do with building and or programming, that’s ok. You’re in the right place. Stop for a second now and think about the concept we just discussed. These statements can all be written symbolically. It’s easy for your brain to deal with the simple concept of a shirt and it’s apparent variable. To simplify, your brain recognizes that each shirt can have 1 color attribute. In the case of a statement where a shirt is Red AND Grey, you know the shirt is multicolored…. and there. You’ve already started creating logical equivalencies.
First, an introduction to symbolic logic. If you are just starting to code, this is your intangible building block to creating vast seas of logic. Basic symbolic logic starts by conceptualizing these concepts we discussed above with the shirts, and turning it into something you can write on paper. For instance “AND” is a symbolic operator. If you have Red AND Grey, both colors need to be present for the statement to be truthful.
The first concept to understand is the concept of True and False. The concepts of true and false in programming are the same as they are in the elementary school classroom. Are you telling the truth? Are all the statements in your argument truthful, or is there one falsehood that corrupts the rest? Statements can be either Truthful or False, there is no in between.
With your concepts of True & False in hand, the next step is to understanding the 5 basic logic operators:
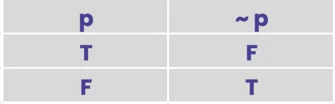
- Not: ~p
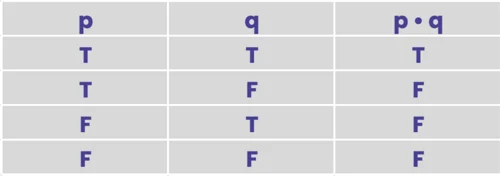
- And: p • q
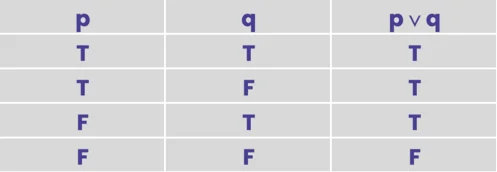
- Or: p ∨ q
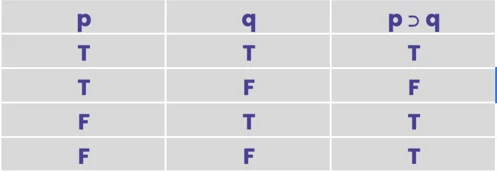
- If: p ⊃ q and
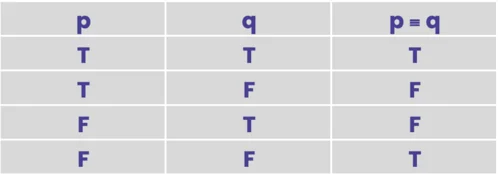
- Equivalency: p ≡ q
Each symbolic operator is as it sounds. The statement “~p” simply negates p. So you would read it “Not P.” In our shirt case we could also right shirt ~red. The “Or” and “And” statements are just as easy to understand. My shirt is red ∨ grey is truthful, but the statement my shirt is red • grey would be false.
We can take the next step with our logic with our other two logical operators. Let’s assume for a minute that I wear the same shirt every Monday while I write our blog. It’s grey. Now we can say Monday Shirt ≡ Grey, my Monday Shirt is Grey. Or I could also say, Monday Shirt ⊃ Grey. If I’m wearing my Monday shirt, for the statement to be truthful, it has the color Grey.
If you are just getting started, it may be each logical operator can be summarized in a truth table. This shows each argument with a mixture of variables and the resulting true or false outputs (noted T or F).
- Not: ~p
- And: p • q
- Or: p ∨ q
- If: p ⊃ q and
- Equivalency: p ≡ q
Creating Logical Statements
Once you have the basics down, you can start creating more complex expressions. Our shirt example is easy to understand, so let’s mix in some variables. If I told you that a shirt had more than one color, you logically understand the shirt will have more than one color as a property. We can also start to think about our shirt’s other attributes. Maybe it’s made of cotton, has 3 buttons, and a collar.
Think about this statement: If I’m wearing a dress shirt then….
- The shirt has buttons
- The shirt requires ironing or dry cleaning
- The shirt is too fancy to wear to my local dive
Now see how we can start to build on this logically? By understanding one piece of information, we can start to write logic based rules. For instance, when I wear a dress shirt, I have to go home and change if I want to go to the dive bar, and need to iron or pay special attention when doing my laundry.
Your building efforts are the same way. Think about building standards, these are all conditional statements and can be codified with logic. Basic examples include the fact that you probably have very different window and lighting standards for your bathrooms. Afterall, no one wants a huge bay window in a toilet cubicle.




